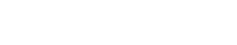DHDAS隨機子空間法模態分析功能
發布時間：2021-07-07
瀏覽量：
隨機子空間識別法是一種先進基于環境振動模態參數識別的時域方法，也是近年來國內外模態分析專家和學者討論的一個熱點。該方法結合了系統識別、線性代數和統計學的理論，通過矩陣計算，從狀態空間方程中識別動態系統，適用于環境激勵條件下結構模態參數的識別。該方法不但能準確識別系統的頻率，而且能很好的識別系統的模態振型和阻尼，使識別結果更有意義和實用價值。
SSI方法基于離散時間狀態空間方程，是直接處理時間序列的時域方法，輸入由隨機白噪聲代替。對于處在環境激勵情況下的土木工程結構而言，在實際測量過程中，環境激勵是不可測量的隨機激勵（輸入），而且強度基本和噪聲影響相似，無法將兩者區分清楚。
因此，將輸入項和噪聲項合并可以得到隨機子空間方法的基本模型—離散時間隨機狀態空間模型：
建立了離散時間隨機狀態空間方程后，需要根據測量得到的響應數據識別出系統矩陣A與輸出矩陣C，進而得到系統的模態頻率、阻尼與振型向量。
本文以某長江大橋實測數據為例，簡要說明DHDAS隨機子空間模態分析功能的操作流程與技術特點，結構模型建立、參數保存、振型展示、模態驗證等模態通用操作功能不在本文贅述。
第一步：結構模型建立
第二步：測試數據選擇。
第三步：確定數據長度（數據起止時刻），生成Hankel矩陣。
第四步：由Hankel矩陣生成Toeplitz矩陣，并對Toeplitz矩陣進行奇異值分解，得到“奇異值—模型階數”曲線。確定系統模型的階數，該階數決定了后續穩定圖計算的最高階次。
影響奇異值分解的噪聲主要包括：
① 模型的不準確性。實際系統對于激勵的反應，不一定100％滿足隨機狀態空間模型，由此會造成一定誤差。
② 測量誤差。在實際測試中由于測試環境的影響和傳感器等測試儀器的影響，測量誤差是不可避免的。
③ 計算時數值精度引起的誤差。
④ 試驗采集的數據總是有限的，模型的輸出協方差需要采用近似估算。
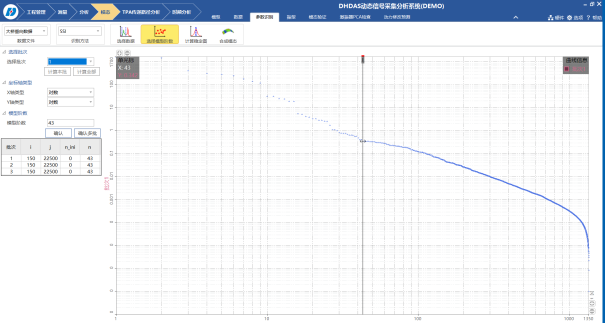
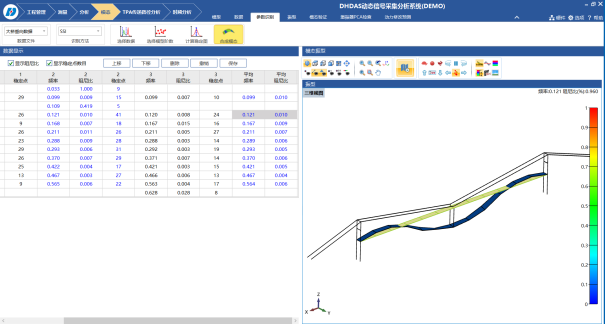
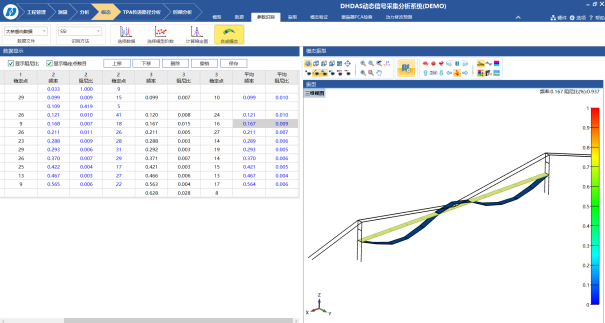
第五步：由Toeplitz矩陣奇異值分解得到的結果可以求解系統狀態矩陣，生成穩定圖，進而求解得到頻率、阻尼與分塊振型向量。
穩定圖把不同階數模型的模態參數畫在同一幅圖上，在相應于某階模態的軸上，高一階模型識別的模態參數同低一階模型識別的模態參數相比較，如果特征頻率、阻尼比和模態振型的差異小于預設的限定值，則這個點就稱為穩定點，組成的軸稱為穩定軸，相應的模態即為系統的模態。
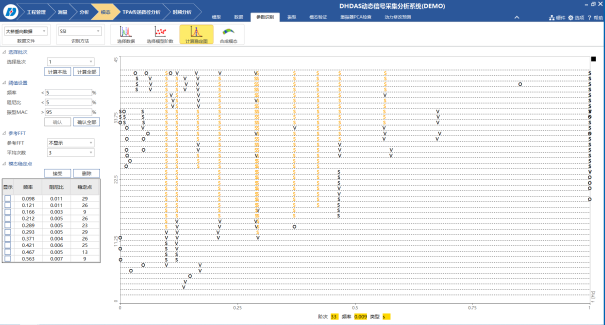
第六步：將由每組測試數據辨識得到的頻率、阻尼與部分振型向量進行組合，得到最終的頻率、阻尼與振型。
最新新聞
在線留言 
工作時間：周一 ~ 周五 / 8:00-17:00
Copyright © 2022 江蘇東華測試技術股份有限公司 All Rights Reserved. 
蘇ICP備18042773號-1 蘇公網安備 32128202000487號 網站建設：中企動力 常州 SEO 基于故障診斷和健康管理的智能設備維保管理平臺
聯系我們 | 法律聲明